回溯算法 - 寻找矩阵中的路径

前言

给定一个矩阵和一个字符串，如何从矩阵中寻找出这个字符串在矩阵中的路径？本文就跟大家分享下如何使用回溯法来解决这个问题，欢迎各位感兴趣的开发者阅读本文。

实现思路

我们先从题目给出的条件入手，逐步分析得出思路，矩阵就是一个二维数组，字符串可以切割成一个数组，我们要做的就是按顺序取出字符串中的每个字符，判断其是否在矩阵中，能否组成一条完整的路径出来。

举例分析

现有一个矩阵（如下所示），有一个字符串bfce，我们需要从矩阵中找出这个字符串在矩阵中所连接起来的路径。

a  b  t  g
c  f  c  s
j  d  e  h

我们从矩阵的[0][0]位置作为入口开始寻找，要查找的第1个字符为b：

0,0 位置的元素是a，与目标值不匹配，继续寻找0,1位置
0,1 位置的元素是是b，与目标值匹配，继续查找第2个字符f
- 更新寻找方向，向下查找
1,1 位置的元素是f，与目标值匹配，继续查找第3个字符c
- 更新寻找方向，向下查找
2,1 位置的元素是d，与目标值不匹配，回到上一步1,1位置
- 更新寻找方向，向上查找，
- 0,0位置的值已经寻找过了，回到上一步1,1位置
- 更新寻找方向，向右查找
1,2 位置的元素是c，与目标值匹配，继续查找第4个字符e
- 更新寻找方向，向下查找
2,2 位置的元素是e，与目标值匹配，所有字符寻找完毕，该路径存在与矩阵中

保存每一步已找到元素在矩阵中的索引

[2,2]位置
[1,2]位置
[1,1]位置
[0,1]位置

最终路径为：[0][1]、[1][1]、[1][2]、[2][2]

思路分析

通过上述举例，我们可以总结出下述思路：

寻找一个切入点，从第一个字符开始寻找其在矩阵中的位置
进入矩阵后，每一步都会有4个移动方向：下、上、右、左
每移动一个方向，都会判断移动后位置的值是否与当前要查找的字符是否相等
- 如果相等，则标识当前位置的元素为已访问状态，沿着四个移动方向继续寻找下一个字符
- 如果不相等，则回到上一步的位置点，尝试其他的三个方向是否有匹配的元素
重复步骤3，直至所有匹配字符的四个方向都被移动
- 字符串中的全部字符都被找到后，则取出每一步的正确索引位置将其保存起来
- 四个方向都被移动后，仍未找到与字符所匹配的元素，则证明该字符串不存在于矩阵中

注意：我们在矩阵中找到与目标字符匹配的元素后，我们需要将这个位置的元素先存起来，然后再改成. 用于标识这个元素已经访问过了，当所有元素找到后再将存储起来的值进行还原。

实现代码

我们分析出思路后，接下来我们来看下实现代码，代码分为2部分：

主函数，用于参数规则判断、寻找切入点、返回找到的路径
寻找路径函数，用于在矩阵中寻找每一个字符

主函数

主函数接受2个参数：路径矩阵、目标字符串

我们需要先对参数进行判空
遍历矩阵从0,0位置开始寻找路径
路径找到则返回路径索引，否则返回目标路径不存在

代码实现如下：

export default class Backtracking {
  // 目标路径在矩阵中的索引
  private readonly pathIndex: Array<string>;

  constructor() {
    this.pathIndex = [];
  }
  
  public findMatrixPath(
    matrix: Array<Array<string>>,
    target: string
  ): Array<string> {
    if (target === "") {
      this.pathIndex.push("参数错误: 目标路径为空");
      return this.pathIndex;
    }
    for (let i = 0; i < matrix.length; i++) {
      for (let j = 0; j < matrix[i].length; j++) {
        if (this.findPath(matrix, target, i, j, 0)) {
          return this.pathIndex;
        }
      }
    }
    // 未找到
    this.pathIndex.push("目标路径不存在于矩阵中");
    return this.pathIndex;
  }
}

寻找路径函数

寻找路径函数接受5个参数：路径矩阵、目标字符串、要寻找的行、要寻找的列、要寻找的字符索引

首先，我们需要判断下要寻找的行、列是否超越矩阵的界限
矩阵中要寻找的行、列位置的元素与要寻找的字符不相等则直接返回false
判断所有字符是否都查找完成
- 完成的话则存储行、列索引，返回true
- 未完成则保存当前行、列处的值、修改该位置的值为.用于标识为已访问状态
从当前坐标点位置沿着其四个方向：下、上、右、下进行查找
查找完成后保存已找到字符的坐标点，还原当前位置所保存的值

代码实现如下：

  private findPath(
    matrix: Array<Array<string>>,
    target: string,
    row: number,
    col: number,
    index: number
  ): boolean {
    // 边界条件判断
    //  1. 行、列值越界直接返回false
    //  2. matrix[row][col]位置的元素与当前要查找的字符不等，证明这个路径走不通
    if (
      row >= matrix.length ||
      row < 0 ||
      col >= matrix[0].length ||
      col < 0 ||
      matrix[row][col] != target[index]
    ) {
      return false;
    }
    // 所有字符都已查找完成
    if (index === target.length - 1) {
      // 保存最后一个字符在矩阵中的坐标
      this.pathIndex.unshift(`[${row}][${col}]`);
      return true;
    }
    // 保存当前坐标值
    const tmp = matrix[row][col];
    // 修改当前坐标的值，标识当前坐标点已经被寻找
    matrix[row][col] = ".";
    // 开始递归: 沿着当前坐标的上下左右4个方向查找
    const res: boolean =
      this.findPath(matrix, target, row + 1, col, index + 1) ||
      this.findPath(matrix, target, row - 1, col, index + 1) ||
      this.findPath(matrix, target, row, col + 1, index + 1) ||
      this.findPath(matrix, target, row, col - 1, index + 1);
    // 本轮递归完成，找到了当前要查找字符在矩阵中的位置
    if (res) {
      // 保存当前要查找字符的坐标点
      this.pathIndex.unshift(`[${row}][${col}]`);
    }
    // 递归完成，复原当前坐标
    matrix[row][col] = tmp;
    return res;
  }

完整代码请移步：Backtracking.ts

编写测试用例

接下来，我们将上述例子代入我们实现的函数中，测试下是否正确。

import Backtracking from "../Backtracking.ts";

const pathArr = [
  ["a", "b", "t", "g"],
  ["c", "f", "c", "s"],
  ["j", "d", "e", "h"]
];
const target = "bfce";
const backtracking = new Backtracking();
const findResult = backtracking.findMatrixPath(pathArr, target);
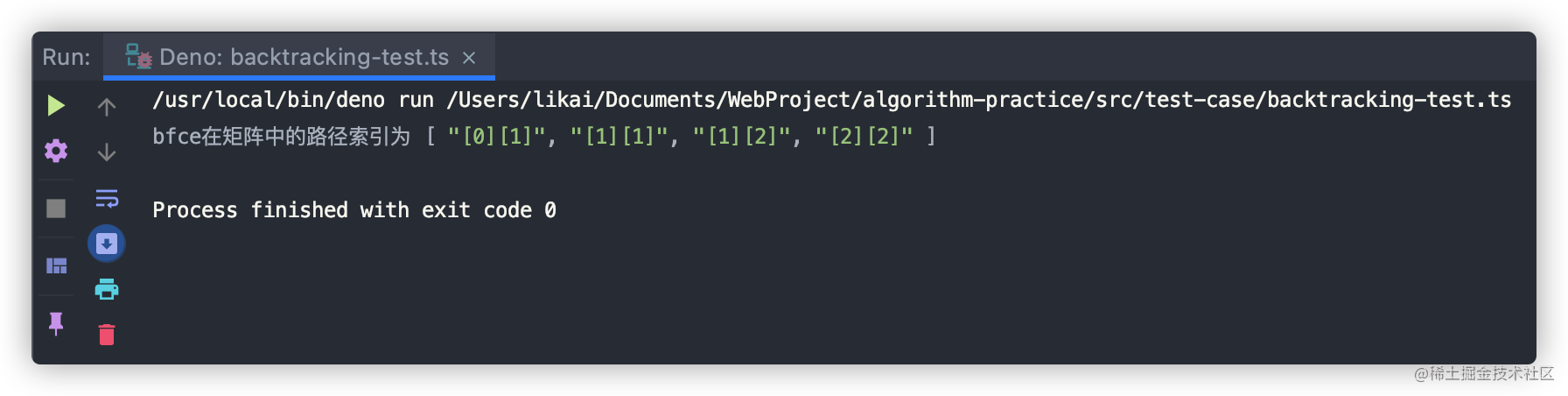
console.log(`${target}在矩阵中的路径索引为`, findResult);

执行结果如下所示：

写在最后

至此，文章就分享完毕了。

我是神奇的程序员，一位前端开发工程师。

如果你对我感兴趣，请移步我的个人网站，进一步了解。

文中如有错误，欢迎在评论区指正，如果这篇文章帮到了你，欢迎点赞和关注😊
本文首发于掘金，未经许可禁止转载💌