前言
给定一颗二叉树的前序遍历和中序遍历的数组,且数组中不包含重复的数字,根据给定的两个数组求出这颗二叉树,这就是重建二叉树问题的定义。
本文将详解重建二叉树问题的解题思路以及其代码实现,欢迎各位感兴趣的开发者阅读本文。
问题描述
我们根据题目的定义来捋一下我们的已知条件以及要解决的问题:
- 二叉树的前序遍历数组和中序遍历数组
- 数组中不包含重复数字
- 根据上述条件重建二叉树
题目分析
乍一看,貌似得不到什么有用的信息,那我们就用一个例子结合题目的已知条件来分析下,看看能不能得到有用的信息。
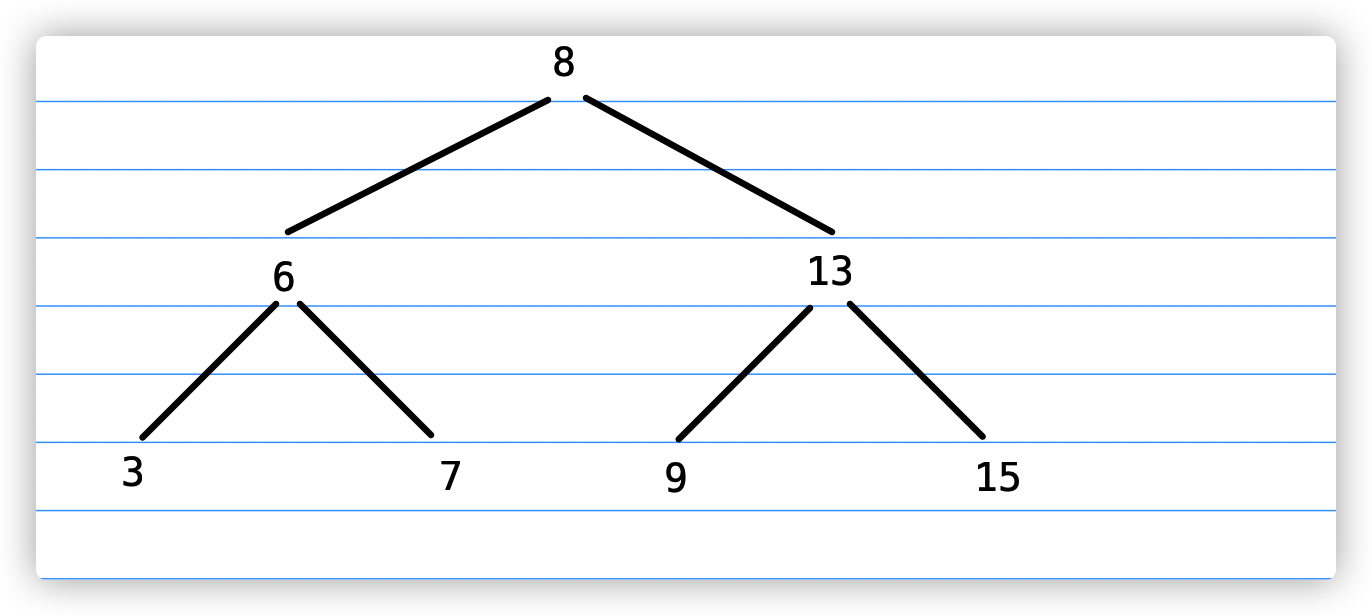
如下图所示,我们画了一颗二叉树:
我们来回顾下前序遍历和中序遍历的规则:
- 前序遍历,先访问根结点,随后访问左子节点,最后访问右子节点
- 中序遍历,先访问左子节点,随后访问根结点,最后访问右子节点
我们根据上述遍历规则,可得出其两种遍历的元素排列,如下所示:
前序遍历: 8 -> 6 -> 3 -> 7 -> 13 -> 9 -> 15
中序遍历: 3 -> 6 -> 7 -> 8 -> 9 -> 13 -> 15
更多有关树的知识可移步我的另一篇文章:TypeScript实现二叉搜索树
我们观察前序遍历和后续遍历的组合后,可得出下述信息:
- 树根结点的值是8
- 8位于中序遍历组合的第3号位置
- 中序遍历组合中,8的左边是它的左子节点,剩余的就是8的右子节点。
- 前序遍历组合中,8的右边3个元素是它的左子节点,剩余的元素是它的右子节点。
我们发现只要根结点在中序遍历组合的位置,就能确定它的左子节点和右子节点。
实现思路
我们观察树中的每个节点后,发现它们都符合我们上面分析出来的信息,因此我们可以根据树中的每个节点求出它的左子节点和右子节点。
由于树中的每个节点都可以用相同的逻辑求出它的左、右子节点,满足了递归要素,因此我们可以用递归来实现。
更多有关递归的知识,可移步我的另一篇文章:递归的理解与实现
我们来分析下递归的基线条件:
- 前序遍历和中序遍历的组合其中任意一个为空时,代表它没有子节点了,返回null。
知道基线条件后,我们就可以来实现这个递归函数了。
- 首先,我们要从前序遍历组合中获取根结点元素
root - 随后,根据
root构建一个树节点tree - 求出root在中序遍历组合中的位置
index - 递归求出
node的左子节点 - 递归求助
node的右子节点 - 最后,
node的左、右子节点都求出来后,将tree返回,出栈,直至栈内元素被清空,二叉树重建完毕,问题解决。
在递归求
node的左、右子节点时,他的前序遍历与中序遍历的组合就是我们之前分析出来的根结点的左右子节点的求法。
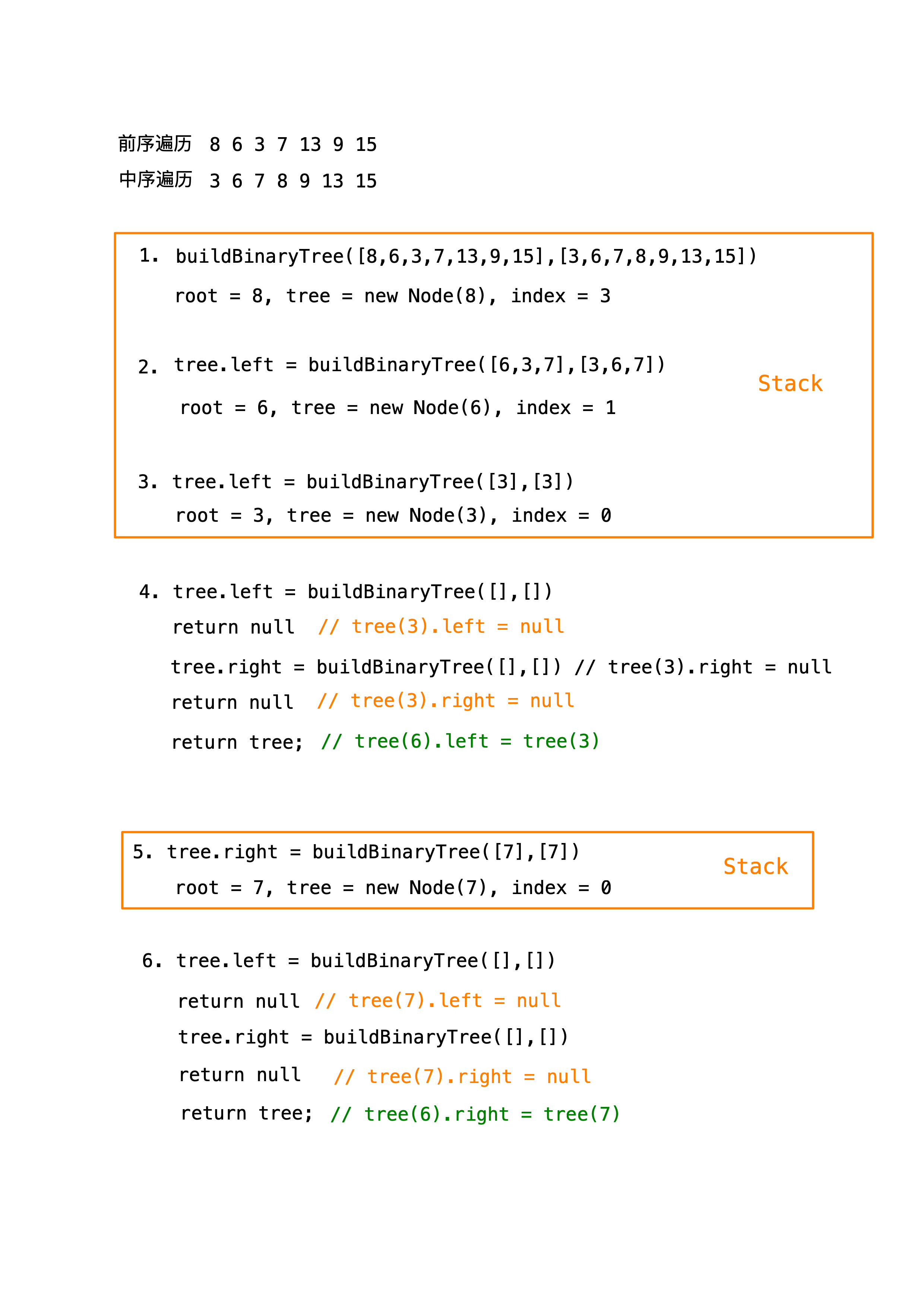
我们通过一个例子,来验证下上述思路是否正确,如下所示:

实现代码
我们有了思路后,接下来接可以用TypeScript将其实现了。
- 新建一个
TreeOperate.ts文件 - 声明TreeOperate类
export class TreeOperate<T> {
}
- 实现重建二叉树函数
buildBinaryTree(prologueArr: T[], middleOrderArr: T[]): Node<T> | null {
// 递归基线条件
if (prologueArr.length === 0 || middleOrderArr.length === 0) {
return null;
}
// 根结点元素
const root = prologueArr[0];
// 根据根结点元素构建树节点
const tree = new Node(root);
// 获取根结点在中序遍历中的位置
let index = 0;
for (let i = 0; i < middleOrderArr.length; i++) {
if (middleOrderArr[i] === root) {
break;
}
index++;
}
// 递归填充它的左子树
// 在前序遍历中,根节点后面的index个元素及时它的左子树,剩余的就是它的右子树
// 在中序遍历中,根结点左边的节点就是左子树,剩余的就是它的右子树
// 因此,当前节点的前序遍历结果为前序遍历的1号位置到index位置(包含index)的元素
// 因此,当前节点的中序遍历结果为中序遍历的0号位置index位置
tree.left = <Node<T>>this.buildBinaryTree(prologueArr.slice(1, index + 1), middleOrderArr.slice(0, index));
// 递归填充它的右子树,左子树已经填充完成剩余的就是右子树,index+1到它的末尾
tree.right = <Node<T>>this.buildBinaryTree(prologueArr.slice(index + 1), middleOrderArr.slice(index + 1));
// 返回tree,出栈,直至栈内元素被清空,二叉树重建完毕,问题解决。
return tree;
}
上述代码地址:TreeOperate.ts
编写测试代码
我们将上图中的例子放进代码中验证下我们实现的函数是否正确执行。
import { TreeOperate } from "./lib/TreeOperate.ts";
const treeOperate = new TreeOperate();
const result6 = treeOperate.buildBinaryTree([8, 6, 3, 7, 13, 9, 15], [3, 6, 7, 8, 9, 13, 15]);
console.log(result6);

写在最后
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于掘金,未经许可禁止转载💌



评论区